今年も3.11を迎えるにあたり、日本統計技術研究所が本部を構える首都圏の直下型地震の発生確率の算出法を復習してみたいと思います。
首都直下で発生する地震について、中央防災会議地震防災対策強化地域指定専門委員会検討結果報告(平成4年8月)では、今から25年前に次のように説明しています。
●この地域では今後 100 年から200年先に発生する可能性が高いと考えられる相模トラフ沿いの規模の大きな地震に先立って、プレート境界の潜り込みによって蓄積された歪みのエネルギーの一部がマグニチュード7 程度の地震として放出される可能性が高いと推定される。
●関東大地震の発生後、既に70年が経過していることを考慮すると、今後その切迫性が高まってくることは疑いなく、次の相模トラフ沿いの規模の大きな地震が発生するまでの間に、マグニチュード7程度の地震が数回発生することが予想される。
特定の地域(内陸)の直下に存在する活断層がずれたり、落ち込んだりすることで起きる地震は、範囲は狭くても(被害範囲も20キロメートルから30キロメートル程度)、揺れは極めて激しくなることがあるとされています。いわゆる、内陸型地震と呼ばれる地震で直下型の地震です。この直下型地震で発生した有名な大震災は『関東大震災』、『阪神・淡路大震災』や『新潟県中越大震災』などです。関東大地震(関東大震災の原因地震)はマグニチュード7.9、兵庫県南部地震(阪神・淡路大震災の原因地震)はマグニチュード7.3、新潟県中越地震(新潟県中越大震災の原因地震)はマグニチュード6.8と記録されています。
さて、現在話題になっている首都直下地震の発生確率ですが、東京都発行の黄色い表紙の「東京防災」では、第1頁に「30年以内に70%の確率で発生すると予測されている、首都直下地震。あなたは、その準備ができていますか。」と極めて刺激的な名文句で警告を発し、発生確率を明言しています。
このトピックスでは「30年以内に70%の確率で発生する」という根拠を復習したいと思います。
そもそも、この発生確率は地震調査研究推進本部地震調査委員会(平成7年1月17日に発生した阪神・淡路大震災の経験を活かし、地震に関する調査研究の成果を社会に伝え、政府として一元的に推進するために作られた組織)の報告に基づきます。
同調査委員会は、首都直下地震を引き起こす「相模トラフ沿いの地震活動の長期評価」(平成16年8月23日)において、南関東においてプレートの沈み込みに伴い発生するM7 程度の地震を「その他の南関東の地震」として、30 年以内に発生する確率を 70%と公表しました。この値は、南関東において「1885 年から2004年までの119年間に発生したM6. 7~7. 2の5つの地震の平均発生頻度から推定した」と説明しています。
その後、東日本大震災の発生を受けて、平成26年4月25日に第二評価が公表されました。改訂の大きなポイントは、元禄関東地震(1703年)と大正関東地震(1923年:関東大地震)の間の220年間にM7程度の地震が8回発生している経験をもとに、M7程度の地震の平均発生間隔を27.5年として、ポアソン分布を用いて発生確率を算出していることです。
下図は、委員会が検討した地震の発生経過を示したものです。
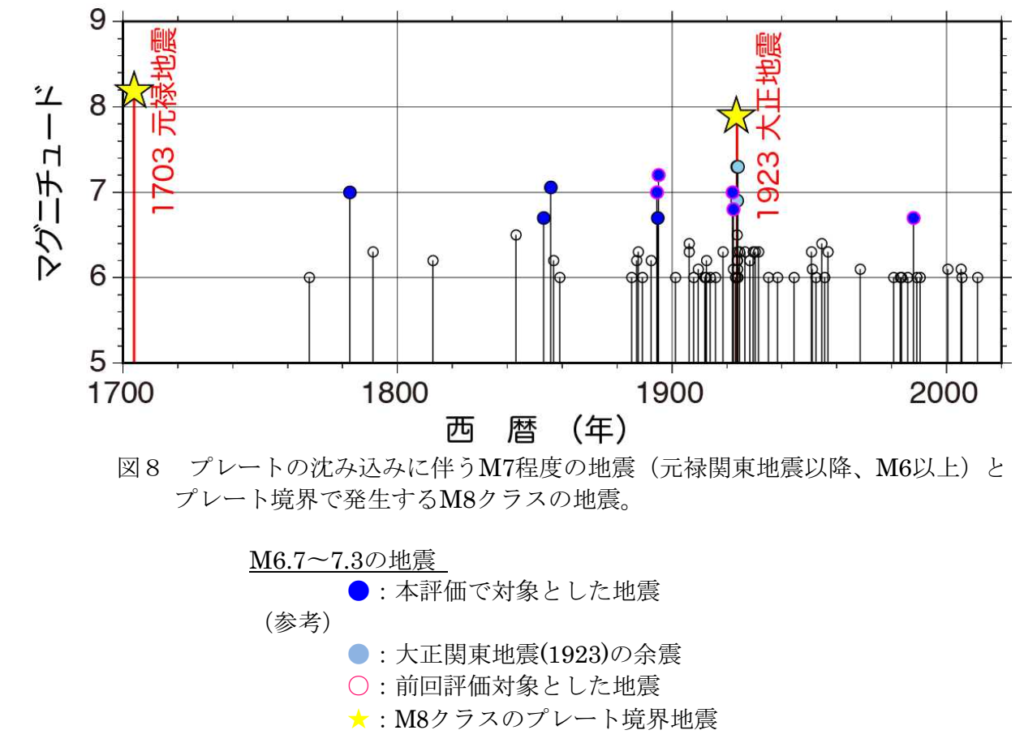
図1 相模トラフ沿いの地震活動の長期評価(第二版)について 平成26年4月25日 地震調査研究推進本部 地震調査委員会 http://www.jishin.go.jp/main/chousa/14apr_sagami/sagami2_shubun.pdf
プレートの沈み込みに伴うM7程度の地震については、特定の震源域で繰り返し発生する地震として扱うことが難しいため、地震調査委員会では下図の太赤線で囲まれる領域内のどこかで発生するものとして発生確率を推定しています。その結果、平均発生間隔は27.5年、30年以内の発生確率は70%程度と推定されたと報告していますが、その計算式を確認したいと思います。
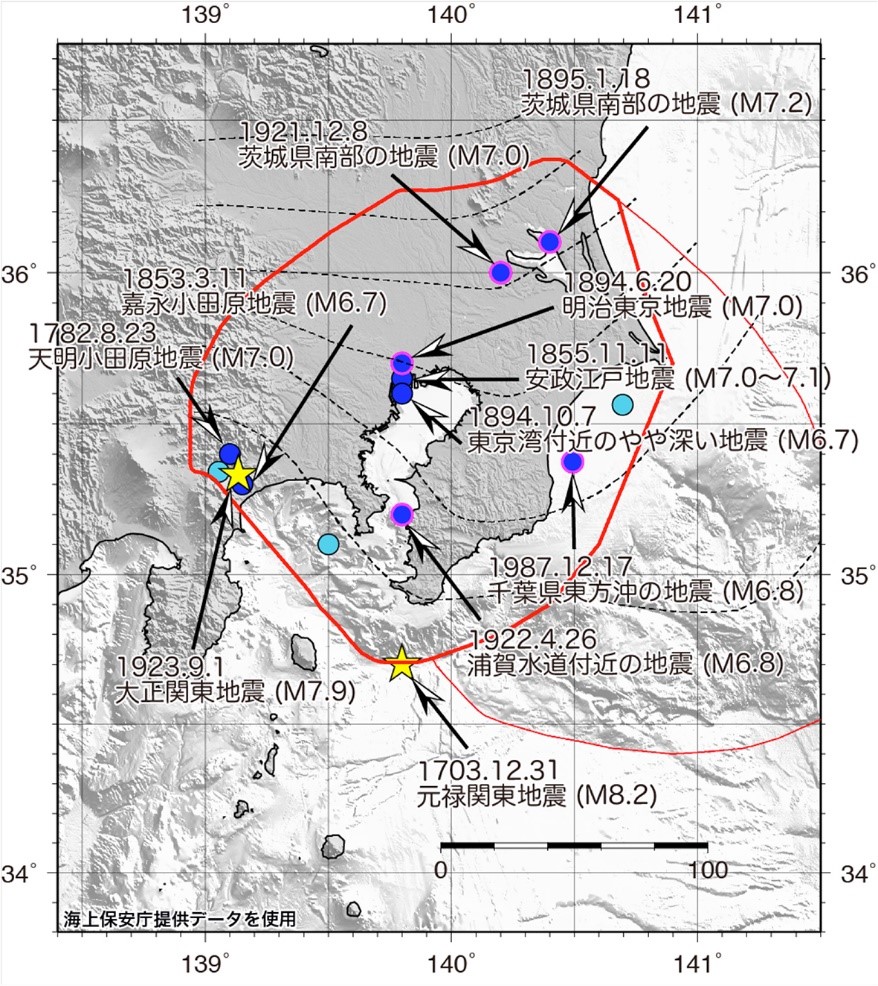
図2 評価対象としたプレートの沈み込みに伴うM7程度の地震
太赤線で囲まれた範囲が評価対象領域を示す。およそ半径150km
細赤線は最大クラスの地震の震源域を示す。
●:本評価で対象とした地震 ●:大正関東地震(1923)の余震
○:前回評価対象とした地震 ★:M8クラスのプレート境界地震
地震調査研究推進本部HPより http://www.jishin.go.jp/resource/column/kohyo_sum_kohyo_sum/
地震調査委員会が発生確率の計算に用いたポアソン分布とは、離散分布の一例であり、簡単に云うと起こる確率が十分に小さい現象の回数を、長期間観測するときの分布を指します。数学者シメオン・ドニ・ポアソンが1838年に確率論とともに発表した確率分布で、1年に何人の兵士が馬に蹴られて死ぬかの確率の分布計算に初めて用いられたと言われています。また、サッカーのワールドカップの得点や交通事故による死者数別の日数の分布などが該当すると報告されています。
そのポアソン分布の式は下記の通り定義されます。
単位時間中にある事象が発生する平均回数をλとするとき、単位時間中にその事象がx回発生する確率密度P(x)は、ポアソン分布に従う。
λ^x
P(x)=── exp(-λ) eは自然対数の底=2.7182
x!
首都圏でM7程度の地震が平均27.5年間隔で発生する場合、期間27.5年での平均発生回数は27.5/27.5=1回となります。期間10年での平均発生回数は10/27.5=0.3636回、期間30年での平均発生回数は30/27.5=1.0909回となります
10年間での発生確率をポアソン分布の式に当てはめる場合、まず、発生しない確率(すなわち単位時間中にその事象が0回発生する確率)を求めます。発生する平均回数は0.3636回ですのでλ=0.3636、発生する回数は0回ですので x=0、をポアソン分布の式に代入すると
λ^x 0.3636^0
P(x)=─── exp(-λ)= ───── exp(-0.3636 )= 0.6952 ・・・ 10年間地震が発生しない確率
x! 0!
となります。
よって、10年間で地震が発生する確率は、1-0.6952 = 0.3048ですので、約30%と求まります。
同様に30年間に地震が発生しない確率は、発生平均回数は1.0909回ですので、x=0、λ=1.0909をポアソン分布の式に代入すると、
λ^x 1.0909^0
P(x)=─── exp(-λ)= ───── exp(-1.0909 )= 0.3359 ・・・30年間地震が発生しない確率
x! 0!
となります。
よって、30年間で地震が発生する確率は、1-0.3359 = 0.6641ですので、約70%と求まります。
東京防災による「30年以内に70%の確率で発生する予測されている、首都直下地震。あなたは、その準備ができていますか。」の問いかけは、今から30年後までに70%の確率で首都直下地震が発生すると言っているのではありません。平均27.5年で発生する地震をポアソン分布に当てはめると、30年間というスパンではその発生確率は70%だと言っているに過ぎません。大正関東地震(1923年)以降現在に至る94年間でみると、M7程度の地震は千葉県東方沖地震(1987年)のみで、90年間に2回しか発生していませんが、1923年からは今年で94年、1987年からでも今年で30年を迎えることを考えると、次の地震は目の前に来ています。ただし、上記の図2の太赤線で示す様にその地震はおよそ半径150kmの広大な首都圏のどこかで発生するもので、我々の足元で発生するか、あるいは遠く離れた場所で発生するかは分かりませんが、足元で発生する前提で準備が必要なことは間違いないと思います。
TOKYO X DAYは決して30年後の話では無いのです。