2016年12月10日(土)夜10時から放映されたTBSの新・情報7days・ニュースキャスターの「ビートたけしの刮目ニュース」で「50人いたら97%の確率で同じ誕生日の人がいる」という予想に反する意外な確率が紹介され話題になっています。
これは「誕生日のパラドックス」と呼ばれる有名な確率で、人の自然な感覚からして不思議な気持ち(一種の錯覚)を起こさせる確率の代表的なものです。このパラドックスのポイントは自分と同じ誕生日の人間がいる確率ではなく、自分も含めた全員の中で同じ誕生日の人が1組いる確率だからです。
「誕生日のパラドックス」としてwikipediaにも紹介されています。
https://ja.wikipedia.org/wiki/
上記の確率を求める問題やその類似問題は、誕生日問題とよばれています。教室に49人の生徒がいるとします。私がその教室に入ったときに、「私と同じ」誕生日の人がいる確率はもちろん50%ではなく、その確率はずっと低くなります。でも、「50人いたら97%の確率で同じ誕生日の人がいる」と言われると、「え~」と思うのは、「私以外の人」同士の誕生日が同じであるという確率が考慮されないからです。
それでは、n人の生徒の中で同じ誕生日の生徒が少なくとも2人いる確率を計算してみます。このとき、双子や三つ子はいないとし、人の誕生日は早生まれが多いとは言いますが、ここでは等しい確率で365日の誕生日が発生しているとします。
このような「少なくとも」という確率問題を考えるときは、まずn人の誕生日が全て異なる場合の確率 p1 を求めます。
2番目の生徒が1番目の生徒と異なる誕生日を持つ確率は、364/365 となります。次に、3番目の生徒が1番目及び2番目の生徒と異なる誕生日を持つ確率は 363/365 で表されます。同じく4番目以降の生徒は 362/365、361/365、……と続き、n番目の生徒は (365-n+1)/365 となります。 すなわち、n人の生徒の誕生日が全て異なる日となる確率は下式で表されます。
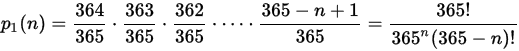
よって、n人の生徒の誕生日の中で同じ誕生日を持つ生徒が少なくとも2人いる場合の確率 p2 は下式となります。
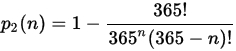
これを解くと、n = 50 のとき、右辺の割り算部分は0.0296(約3%)となります。よって、同じ誕生日を持つ生徒が少なくとも2人いる場合の確率は、p2 =0.9704となり、97%という確率が求まります。
ちなみに、49人の生徒がいる教室に、私が入った場合、私と同じ誕生日を持つ生徒がいる確率 p3 は下式で表されます。
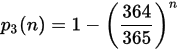
これを解くと、n = 50ですから、p3 = 0.1282となり、約13%となります。
一般の感覚と異なるような数字に「あれ?」と思うパラドクスの1つです。